IPES Research Group @ LNCC
Innovative Parallel finite Element Solvers

This five-lecture course took place as part of the training program of L'École Doctorale en Sciences Fondamentales et Appliquées, at Université Côte d’Azur. The course presented an overview of the origin of the MHM method as well as the MHM's basic theory and practical aspects of the implementation of the MHM method, including practical numerical simulations using the MultiScale FEM Library (MSL).

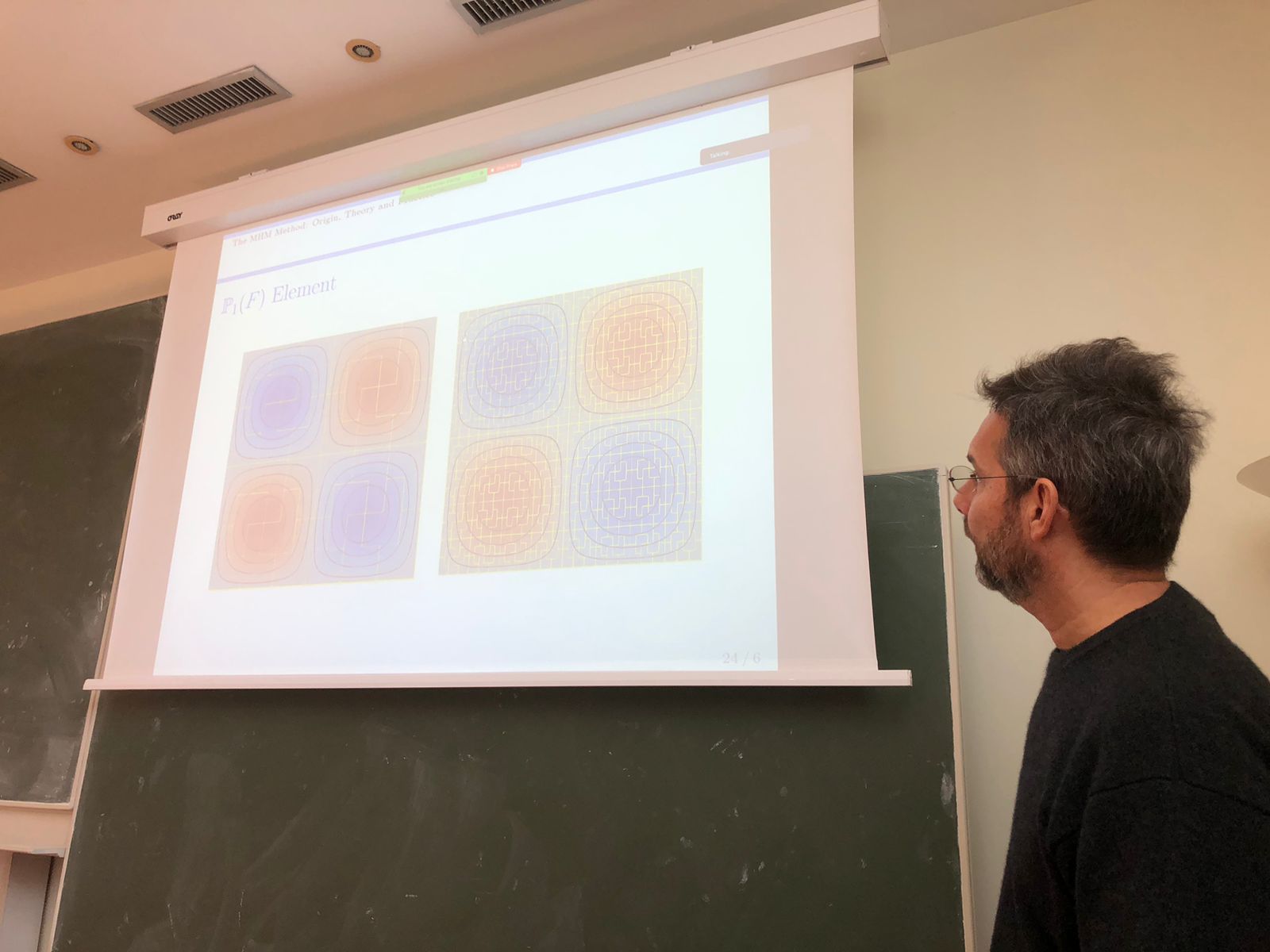
We proposed a new finite element for the mixed multiscale hybrid method (MHM) applied to the Poisson equation with highly oscillatory coefficients. Unlike the original MHM method, multiscale bases are the solution to local Neumann problems driven by piecewise continuous polynomial interpolation on the skeleton faces of the macroscale mesh. As a result, we prove the optimal convergence of MHM by refining the face partition and leaving the mesh of macroelements fixed. This property allows the MHM method to be resonance free under the usual assumptions of local regularity.

Larissa Martins was the first place winner of the SBMAC Odelar Leite Linhares Award, Masters category (2021), for her dissertation "A Petrov-Galerkin Multiscale Hybrid-Mixed Method for the Darcy Equation on Polytopes". Larissa was supervised by Professors Frédéric Valentin (LNCC) and Honorio Fernando (UFF).

The research project EOLIS — Efficient Off-Line Numerical Strategies for Multi-Query Problems —, formed by researchers and students from the IPES and NUMA Research Groups at LNCC, and coordinated in Brazil by Frédéric Valentin, was selected in the new Math-Amsud 2020 call. STIC-AmSud and Math-AmSud are regional cooperation programs between France, Argentina, Bolivia, Brazil, Chile, Colombia, Ecuador, Paraguay, Peru, Uruguay and Venezuela. The objective is to implement joint projects and strengthen collaboration in the areas of Science and Information and Communication Technology, in the first, and in Mathematics, in the second. The approved projects last two years and involve at least two South American countries and one or more teams of French scientists.

The EOLIS project will receive funding from CAPES during the period 2021-2022, including post-graduate and post-doctoral scholarships. International collaboration involves INRIA from France, Universidad de Concepción and Universidad Católica de la Santísima Concepción from Chile, in addition to LNCC.

"The EOLIS project aims to develop new high-performance numerical and computational algorithms for the resolution of physical / biological models, which require a huge range of computational simulations due to large variations in the model data. A typical application is the numerical approximation of model solutions based on stochastic differential equations. This project strengthens the cooperation between leading research groups in scientific computing in France, Chile and Brazil and constitutes a natural development of the PHOTOM project ( Math-Amsud 2018-2020). ", emphasizes Frédéric Valentin.

Frederic Valentin has been awarded a grant in FAPERJ's "Scientist of Our State 2020 - CNE" Program. His project aims to develop and mathematically analyze new multi-scale finite element methods, which give rise to new computational algorithms adapted to new generations of massively parallel computers. Such algorithms aim to solve systems of differential equations with heterogeneous and/or singularly disturbed coefficients.

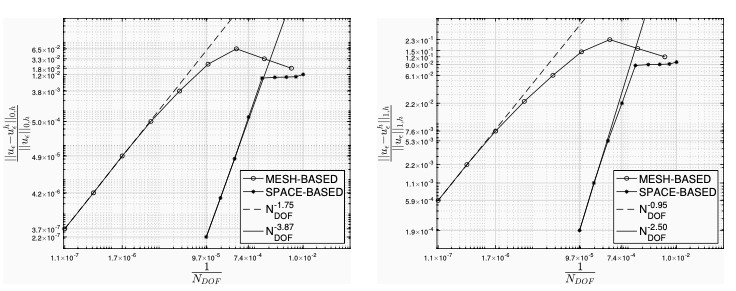
We proposed a new family of polytopal finite elements for the MHM method applied to the linear elasticity model in bidimensional and tridimensional problems. We extended the construction and the analysis of the MHM method proposed in other pieces of work that approached these problems using only simplx finite elements. We proved optimal convergence in the L2 norm using these polytopal finite elements. We also addressed computational aspects of this new family of methods, developed for running in parallel with different configurations, and we illustrated by means of computational experiments how to balance the execution time and the memory consumption in search for a certain approximation order. More information.

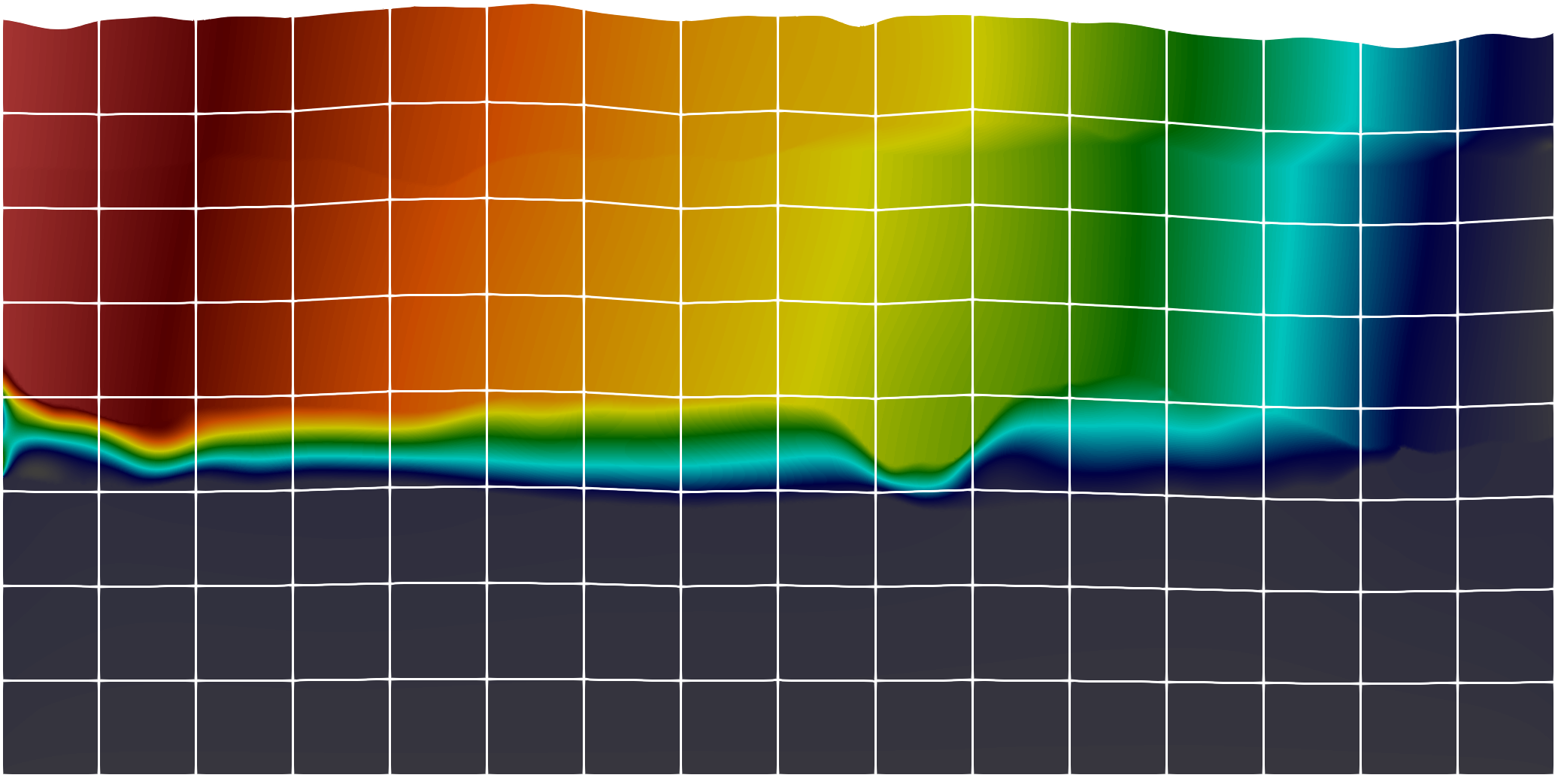
The figures above show the x and z components of displacement obtained for a linear elasticity model with the MHM method in a domain with null displacement in the bottom boundary and null traction in the remainder boundaries. The domain is divided into 16 layers according to the HPC4e benchmark, with layers 4 and 12 containing saturated clay and the other layers filled with the original materials from the benchmark. The source is the piecewise weight, using gravity acceleration of 9.8 m/s2. The employed mesh is rectangular throughout the domain (note how the layers "cross" the elements of the mesh), except for the top boundary, in which elements with an average of 35 edges are used for capturing the topography.